New research reveals factors that influence the lifetime of electronics and outlines a model for physical failure mechanisms.

By Francesco Iannuzzo, Ionut Vernica and Per Thåstrup Jensen

"Reliable product development based on physics of failure", a 3-year project, has revealed factors that influence the lifetime of electronics and explored the possibility of creating a mathematical acceleration model for physical failure mechanisms.

One of the challenges in doing so is determining the acceleration model and the mathematical coefficients that are part of it. Aalborg University (AAU) has taken some preliminary steps toward this model.

Stressors and lifetime calculation

The lifetime of electronics is influenced by electrical effects, such as large pulse currents in components. In the worst-case scenario, these can lead to explosion or combustion. Impulse currents as stressors are part of the electrical mission profile that a product experiences during its lifetime.

In a Ph.D. project, AAU has worked on modelling a passive component: the metal-oxide varistor (also called a "MOV").

Characterising physical conditions

When a varistor is exposed to a short-term overvoltage (a transient), it causes the component to become heated. It is straightforward to create a mathematical model for the energy dissipation in the component, and to thus calculate the expected increase in temperature. The increase in temperature can then be taken as the input for a lifetime estimate of the component with short-term temperature increases as a stressor.

In practice, multiple physical conditions must be accounted for in modelling. The thermal capacity of (e.g.) zinc oxide is temperature-dependent, increasing by a factor of about 40% for temperatures up to 1500 K. Zinc oxide's ability to dissipate heat varies even more, and reduces by a factor of almost 10 over the same temperature range.

This means that a thermal model must be based on these nonlinear conditions, and that temperature increase calculations must be performed using nonlinear models, in which an algorithm divides the calculation into small time steps. Each step involves looking up coefficients in tables, as well as the summation of partial calculations.

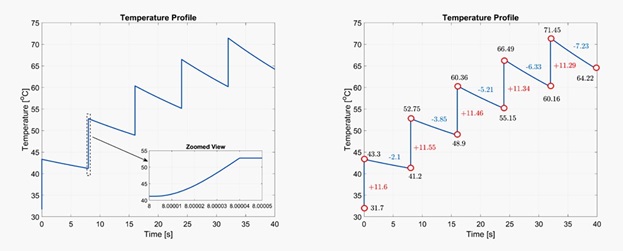
Validating the model

Future work on the project will include a validation of the simulation model, which is based primarily on empirical data. One way to illustrate the model is shown in figure 1, in which stepped increases in temperature can be evaluated using thermographic surface temperature measurements and adjustments to the model's parameters. Doing so accounts for the cumulative effect of the entire component's volume.

Illustration, physics of failure mechanisms
Figure 1: Temperature shown versus time, illustrating rapid temperature rise at each impulse and a cooling process between impulses. Note that each impulse accumulates energy in the component, resulting in stepwise rise in temperature.